Homogeneous Coordinates
撰写于 2020-11-08 修改于 2021-07-07 views
Homogeneous Coordinates
What are homogeneous coordinates?
Homogeneous coordinates are a coordinate system for projective spaces and allow us to express things very elegantly if we work with cameras and want to describe how a point from the 3D world is mapped onto my 2D image. They basically have two key advantages. The first one is they can express a variety of transformations as a matrix so whether they can execute this transformation by simply performing a matrix vector multiplication. The second advantage is that in homogeneous coordinates I can express points which are infinitively far away with finite coordinates and again that’s something that’s useful if you work with your cameras. Those two properties make a lot of mathematical derivations much simpler and easier.
In homogeneous coordinates compared to my Cartesian coordinates this is the reason why they are an attractive tool it especially used for disciplines that work with cameras such in computer vision or photogrammetry.
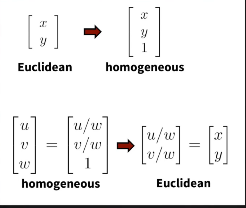
So look into a small example. We have the point [2 ,4] in our Euclidean world and we want to go into homogeneous coordinates. We need to do is we add an additional dimension so we add a third dimension here and fill this dimension with one. This puts this point from the Euclidean world into homogeneous coordinates. And this additional dimension allows us to do those nice things if we want to make back from homogeneous coordinates into the Euclidean world we have to get rid of this additional dimension so what when you want to reduce the third dimension and go back to two dimensions in this example. And before we actually need to divide all the components of the vector in homogeneous coordinates by the last component. the last component becomes 1 again and the last component is 1 and I can just ignore this additional dimension and back in Euclidean world.
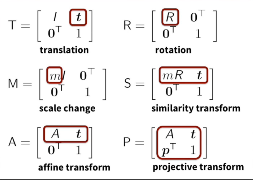
With this additional dimension we can now express a certain type of transformations in an elegant throught a simple matrix. So start with the example of a translation with this very simple matrix if we multiply this matrix where is the vector gets translated by this translation vector t. And so by multiplying a vector with this matrix. This vector gets translated by T and that’s something that I can not in Euclidean world. I cannot only do this translations, I can also do this with a large number of other transformations such as rotations, similarity transforms, _ _ transformations, affine transformations or projective transformations. And this allows me to write them all down in a matrix form and can simply change those transformations in elegant way by just performing matrix multiplications. So by multiplying all those matrices together I get a resulting transformation that resembles this chain of transformations. This is very nice because it allows me to compress a large number of chain transformations into a single matrix and then I just need to execute the matrix vector multiplication in order to transform a point.
So if we have points in homogeneous coordinates, they have special properties that so-called homogeneous property that means every object in homogeneous property is only defined up to a scalar so I can multiply every object in homogeneous coordinates with a number which is unequal to 0 and it still represents the object. So the vector [2, 4, 1] is identical to the vector [4, 8, 2] for example.
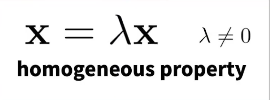
The second nice property that I was referring to was representing points which are infinitively far away so by setting the last coordinates to zero I can express points which are infinitively far away with finite coordinates, so you can see this if you need to divide by the last component if you want to go back the Euclidean world you can see that you would divide by zero and then the points would be infinitively far away. But the attractive thing in homogeneous coordinates is that we will maintain the direction to the point so even if the point is infinitively far away we can still estimate the direction to that point. And this is very relevant with cameras where you have points which are far away potentially infinitively far away while which are at the horizon which in geometric estimation processes all allows you to estimate the orientation of your camera actually quite well but which cannot be handled very well if in my Euclidean world. And therefore going to this projective spaces is very attractive when working with cameras.